Como sei que o ponto faz parte da reta?

Matemática

Você já ouviu aquela expressão “um ponto fora da curva”? Vamos aprender mais sobre um tema parecido com esse: quando um ponto faz parte de uma reta (ou de uma curva qualquer). (Estamos considerando o espaço euclidiano e plano cartesiano).

» Saiba mais sobre os planos

» Posições relativas entre duas retas

» Conjuntos

QUANDO UM PONTO FAZ PARTE DE UMA RETA? E DE UMA CURVA QUALQUER?

Uma reta, ou uma curva qualquer, são a representação gráfica (a forma visual) de apresentarmos uma função f(x). Se um ponto P(X, Y). faz parte de uma função f(x), temos sempre que f(X) = Y, ou seja, quando substituímos X na função, obteremos Y (lembrando que X precisa pertencer ao domínio da função f(x)).

Vamos ver alguns exemplos?

1) O ponto P (0, 1) pertence à reta f(x) = 2x + 1?

Se (0, 1) pertence à reta f(x) = 2x + 1, então Y = 2X + 1.

Y = 1 e X = 0.

Substituindo na função: f(0) = 2 • 0 + 1 = 1

Portanto, f(0) = 1 = Y ✔ e o ponto pertence à reta (veja no gráfico abaixo)!

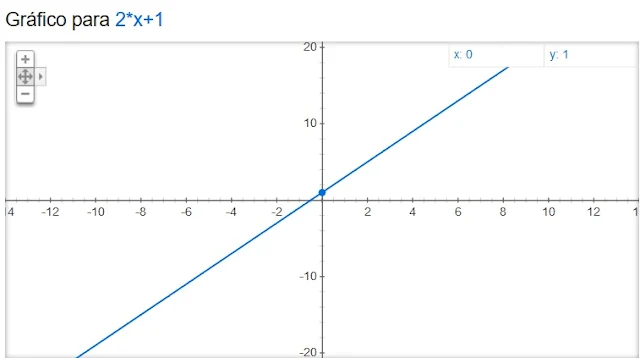[f(0) = 1 = Y ✔ Imagem: Gerador de gráficos do Google]

2) O ponto P (2, 3) pertence à curva f(x) = x² + 2x - 1?

Vamos conferir substituindo X = 2 e vendo se chegamos a Y = f(X) = 3:

f(2) = 2² + 2 • 2 – 1 = 4 + 4 – 1 = 7

f(2) = 7  ≠ Y = 3 ❌

Como Y é diferente de f(X), o ponto P não pertence à curva.

[f(2) = 7  ≠ Y = 3 ❌ Imagem: Gerador de gráficos do Google]

□

👉 E ainda mais para você: Representação das funções

GOSTOU DESTA POSTAGEM ☺? USANDO A BARRA DE BOTÕES, COMPARTILHE COM SEUS AMIGOS 😉!